1) Who was Zipf?
George Kingsley Zipf was an American linguist and philologist, best known for his work on the statistical analysis of language, which led to the formulation of Zipf’s Law. Born in 1902 in Freeport, Illinois, Zipf initially pursued a degree in German philology at Harvard University, where he later earned his doctorate in 1929. His early academic work focused on German literature, but his interests soon expanded to linguistics and quantitative studies of language. Zipf’s intellectual curiosity, combined with his interest in finding patterns in seemingly chaotic systems, led him to explore various fields, including philology, sociology, and mathematics.
Zipf’s career was primarily spent at Harvard, where he held various teaching positions in German and linguistics. His work became increasingly interdisciplinary, straddling the boundaries between linguistics and mathematics. Although much of his early work dealt with traditional language studies, he eventually began to examine the statistical properties of language, particularly how words are used in natural languages. This exploration led to his most notable contribution, Zipf’s Law, a principle that identifies a relationship between the frequency of a word’s usage and its rank in a language.
Beyond linguistics, Zipf was interested in the broader application of statistical principles to human behaviour. He believed that many aspects of human life, including economics, social structures, and even city sizes, followed similar patterns to those found in language. This idea is reflected in his 1949 book, Human Behavior and the Principle of Least Effort, in which he argued that human actions are governed by an overarching tendency to minimise effort in various tasks.
Despite the groundbreaking nature of his work, Zipf’s theories were not immediately recognised as revolutionary. His ideas gained more attention after his death in 1950, as they began to influence a variety of disciplines, from linguistics and information science to physics and economics. Today, Zipf’s Law is widely recognised not only as a foundational concept in computational linguistics but also as a valuable tool for understanding complex systems in other fields.
Zipf’s work laid the foundation for many later developments in the study of language and information. His interdisciplinary approach, combining linguistic data with mathematical analysis, was ahead of its time and paved the way for computational approaches to linguistics. Though some of his broader applications of Zipf’s Law have been met with criticism, particularly in areas where the law does not hold as precisely, his insights into language remain influential.
2) Zipf’s Law:
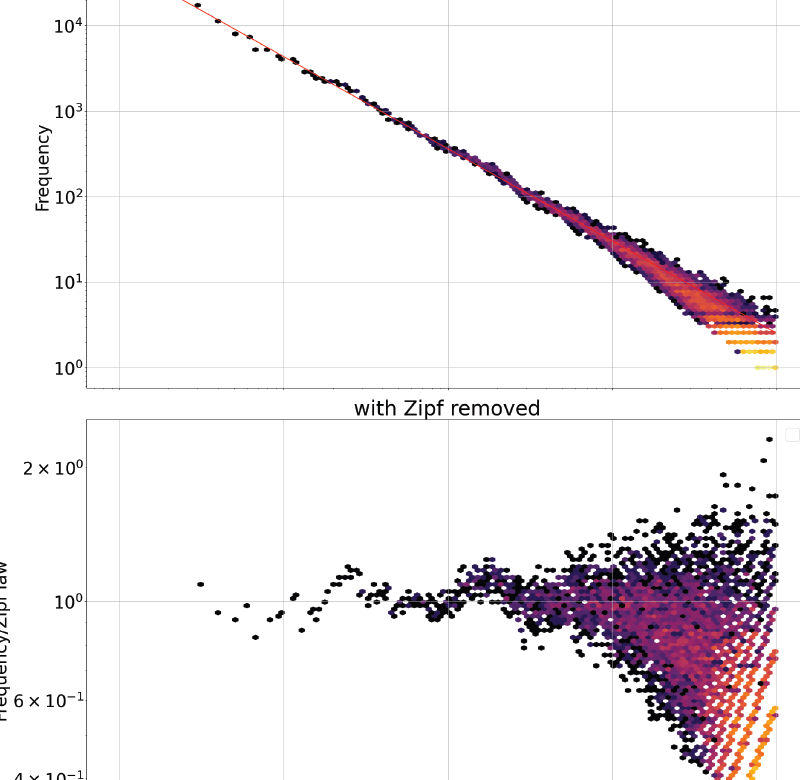
Zipf’s Law is a principle that describes the relationship between the frequency of occurrence and the rank of items within a dataset. Originally formulated in the context of linguistics by George Kingsley Zipf in the mid-20th century, the law posits that in any given language, the frequency of a word is inversely proportional to its rank in the frequency table. In simple terms, the most frequent word in a language will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, and so on. This observation led to Zipf’s assertion that language, and indeed many other systems, follows a predictable and regular distribution.
The classic example of Zipf’s Law in linguistics is the frequency of word usage in English. Words like “the,” “and,” and “of” are among the most commonly used, while more obscure words are used far less frequently. According to Zipf’s Law, if you rank words from the most to least frequent, the second most frequent word will appear half as often as the most frequent one, the third word will appear one-third as often, and so on. This creates a hyperbolic distribution, which, when plotted on a log-log scale, results in a straight line with a slope of approximately -1.
Though Zipf’s Law was first applied to linguistics, it has since been found to describe patterns in a wide range of disciplines, from city populations to internet traffic and even wealth distribution. For example, the size of cities often follows a Zipfian distribution, where the largest city in a country tends to be about twice the size of the second largest, three times the size of the third largest, and so on. This universality makes Zipf’s Law a powerful tool for analysing seemingly disparate phenomena.
One of the reasons for the pervasiveness of Zipf’s Law is that it reflects underlying principles of human behaviour. Zipf himself theorised that the law is rooted in the “principle of least effort,” where both speakers and listeners in a conversation aim to minimise the effort required to communicate. This means that speakers tend to use certain words frequently to convey meaning efficiently, while listeners become familiar with these high-frequency words, making the communication process more streamlined. In this sense, Zipf’s Law can be seen as a manifestation of the economy of language, where a balance is struck between the effort of the speaker and the listener.
Mathematically, Zipf’s Law is often expressed as a power law, where the frequency of occurrence () of an item is proportional to the inverse of its rank i.e., ()∝1/s, where
s is a constant. In many cases, is close to 1, resulting in the classic Zipfian distribution. This power-law behaviour is not unique to language; it is also seen in networks, economics, and natural phenomena. However, it is important to note that while Zipf’s Law holds in many cases, it is not a universal rule. Deviations from the law can occur, particularly in small datasets or those with unusual distributions.
Despite its simplicity, Zipf’s Law has profound implications for fields such as information theory, machine learning, and data science. In information retrieval, for instance, the law can be used to optimise search algorithms by prioritising the most common queries. In machine learning, Zipfian distributions often appear in natural language processing tasks, influencing how algorithms handle word frequency data. Similarly, in economics, the law has been used to describe the distribution of income and wealth, helping to explain why a small percentage of the population often controls a disproportionately large share of resources.
3) Its Applications:
Zipf’s Law, though initially discovered in linguistics, has been found to have far-reaching applications across various fields. Its versatility is rooted in its ability to describe the distribution of items in a wide range of systems, from natural language processing to economics and city planning. The universality of Zipfian distributions makes the law an invaluable tool for researchers and practitioners alike, allowing them to identify underlying patterns in complex systems and optimise processes accordingly. Each application of Zipf’s Law reveals different aspects of how systems organise themselves and the frequency with which certain elements occur.
One of the most significant applications of Zipf’s Law is in computational linguistics and natural language processing (NLP). Given that the frequency of words in any language follows a Zipfian distribution, NLP algorithms often take this pattern into account when designing models for tasks such as speech recognition, machine translation, and text generation. For instance, models like word embeddings, which represent words in continuous vector space, must balance frequent and rare words to avoid overfitting. The knowledge that a small number of words account for most language usage allows developers to create more efficient algorithms by focusing on the most common terms, while also ensuring that rarer words are adequately represented.
In the realm of information retrieval and search engine optimisation, Zipf’s Law is used to optimise the indexing and retrieval processes. Search engines like Google recognise that certain queries are far more common than others and structure their databases accordingly. Zipf’s Law helps predict which terms are likely to be used frequently in searches, enabling better ranking of pages and faster retrieval of information. Additionally, in text compression, knowledge of word frequencies allows for more efficient encoding. Since common words are used more often, they can be represented with shorter binary codes, while less frequent words are given longer codes, thus reducing the overall size of text files.
Zipf’s Law has also proven useful in network theory, particularly in understanding the structure of the internet and social networks. The distribution of web traffic, where a few websites (such as Google, YouTube, and Facebook) account for the majority of internet traffic, follows a Zipfian distribution. Similarly, in social networks, a small number of users or nodes often have disproportionately high numbers of connections, while the majority of users have fewer. This “scale-free” nature of networks is vital for understanding how information spreads online and how viral content can emerge. It also has implications for cybersecurity, as the most connected nodes or websites become key targets for malicious attacks.
Another fascinating application of Zipf’s Law is in urban studies and city planning, where it describes the distribution of city sizes. In many countries, the population size of cities follows a Zipfian distribution, with the largest city often being twice as large as the second largest, three times as large as the third, and so forth. This observation is known as the Rank-Size Rule in urban geography. Planners and economists use this insight to study the growth of urban centres, resource allocation, and the economic relationships between cities. Understanding the rank-size distribution of cities also helps in forecasting future population trends and in designing infrastructure to accommodate urban expansion.
In economics, Zipf’s Law can be applied to the distribution of income and wealth, often described by a Pareto distribution, a concept closely related to Zipfian behaviour. A small proportion of the population controls a large percentage of the wealth, while the majority possesses much less. This phenomenon is sometimes referred to as the “80-20 rule” (where 20% of the population controls 80% of the wealth), and it has profound implications for policies aimed at reducing inequality. Economists utilise Zipf’s Law to model market behaviour, distribution of resources, and even the likelihood of financial crashes by identifying patterns of wealth concentration.
Beyond human-made systems, Zipf’s Law also appears in biology and ecology. For example, in the study of biodiversity, the distribution of species abundances in ecosystems often follows a Zipfian pattern. A small number of species will be very abundant, while the majority are rare. This understanding helps ecologists predict the health of ecosystems, conservation needs, and the potential impact of species loss. Similarly, in genomics, the frequency of certain DNA sequences in the genome often follows Zipf’s Law, aiding researchers in identifying the functional importance of genes or other genetic elements.
Even in the arts and culture, Zipf’s Law can be applied. For example, in literature, the law has been used to analyse the frequency of word usage in the works of specific authors, revealing insights into their style and thematic focus. In music, researchers have found that the popularity of songs or albums follows a Zipfian distribution, where a few hit songs dominate the charts, while the majority receive much less attention. This principle also applies to movie revenues, where a handful of blockbuster films generate the majority of industry profits, a pattern mirrored in many creative industries.
4) Zipf’s Law and Urban Population:
Zipf’s Law has intriguing applications in urban studies, particularly in the distribution of city populations. The law suggests that the size of cities within a country or region follows a predictable pattern, where the largest city is approximately twice the size of the second largest, three times the size of the third, and so on. This relationship between the population size and the rank of cities in a given hierarchy is often referred to as the Rank-Size Rule in urban geography, and it has been found to hold true in many countries across different periods of time. The consistency of this pattern raises significant questions about the forces that shape urban development and population distribution.
In countries where Zipf’s Law closely applies, the largest city tends to dominate the national urban landscape, serving as an economic, cultural, and political hub. For example, cities like Tokyo, New York, and London vastly overshadow the next largest cities in their respective countries, both in terms of population and influence. According to Zipf’s Law, if you rank cities by population, the second largest city will have roughly half the population of the largest, the third largest will have one-third, and so forth. This results in a predictable hierarchy where a few megacities exist alongside a large number of smaller urban centres.
One of the key insights Zipf’s Law offers in the context of urban population is that cities tend to grow according to a self-organising principle, where no central authority directly controls their sizes, yet a stable distribution emerges. Urban economists and geographers use this principle to understand why certain cities grow exponentially, attracting more residents, industries, and services, while smaller cities struggle to expand. The concentration of economic activities, infrastructure, and cultural amenities in larger cities makes them magnets for migration, often at the expense of smaller towns and rural areas. This leads to the uneven urbanisation patterns observed in many countries.
There are several theories that explain why Zipf’s Law holds for urban populations. One prominent explanation is the principle of least effort, which was central to Zipf’s original thinking. The idea here is that people and businesses tend to gravitate towards larger cities because they offer the most opportunities with the least effort. Larger cities provide better infrastructure, more diverse job markets, superior educational institutions, and a richer cultural life, all of which reduce the costs associated with living and working there. This attracts more people and firms, creating a self-reinforcing cycle of growth that is reflected in the city’s population size.
However, Zipf’s Law does not apply universally or in all regions. In some countries, particularly those with highly centralised governments or restrictive urban policies, the distribution of city sizes deviates from the Zipfian pattern. In these cases, political and economic factors may prevent cities from growing according to the self-organising principle suggested by Zipf. For example, countries that have concentrated resources in a single capital city may not exhibit the same rank-size distribution, as smaller cities are stifled from competing with the dominant urban centre. Alternatively, highly planned economies might demonstrate deviations from the law due to controlled growth and migration policies.
Urban planners and policy makers use Zipf’s Law to model and forecast urban growth, providing insights into how cities are likely to evolve in the future. By examining the population distribution across cities, planners can identify imbalances that may require intervention, such as congestion in megacities or underdevelopment in smaller towns. This understanding also helps governments allocate resources more efficiently, ensuring that infrastructure and services are proportionally distributed according to the population hierarchy. In regions where population distribution does not follow Zipf’s Law, planners might investigate whether artificial constraints are hindering the growth of certain cities or if more organic factors are at play.
In addition to its applications in contemporary urban planning, Zipf’s Law can also offer historical insights into the development of urban populations. Many cities that follow Zipfian distributions today have evolved naturally over centuries, with their current population sizes reflecting long-standing economic and geographic advantages. The law thus provides a useful framework for examining how historical migration patterns, trade routes, and industrialisation have shaped the urban landscapes of today. In contrast, regions that have experienced significant disruptions, such as wars or major political upheavals, may display deviations from Zipf’s Law, as cities either grew rapidly due to migration or shrank due to destruction and depopulation.
Interestingly, Zipf’s Law can also be applied to megaregions, where a network of interconnected cities follows a Zipfian distribution across the entire region. For instance, in areas like the Pearl River Delta in China or the BosWash corridor in the United States, a cluster of cities forms a unified economic and social system. In these cases, the population distribution of individual cities may not strictly follow Zipf’s Law, but the overall region often exhibits a rank-size relationship, with a few dominant cities and many smaller ones.
5) Its Legacy:
The legacy of Zipf’s Law extends far beyond its initial formulation in the study of language, leaving a lasting impact across numerous disciplines. As one of the earliest attempts to quantitatively model the complexities of natural language, Zipf’s Law has paved the way for advancements in linguistics, information science, and the understanding of complex systems. Its influence is particularly significant because of its simplicity and universal applicability, offering a framework that transcends individual disciplines and provides insights into the underlying patterns governing diverse phenomena.
In linguistics, the legacy of Zipf’s Law is firmly established as a foundational concept in the quantitative study of language. By demonstrating that word frequencies follow a predictable distribution, George Zipf opened the door for a more scientific approach to understanding language. Today, this insight plays a critical role in areas such as corpus linguistics, natural language processing (NLP), and computational linguistics. Zipf’s Law serves as a guiding principle in developing models that deal with word frequency and usage patterns, such as those used in speech recognition, machine translation, and text prediction technologies. The continued relevance of Zipf’s Law in these fields highlights its enduring importance in the age of artificial intelligence and big data.
Beyond linguistics, Zipf’s Law has left a profound mark on the study of complex systems. The law’s ability to describe rank-size distributions in diverse settings, from city populations to internet traffic, has made it an essential tool for researchers in fields such as economics, sociology, and urban studies. The discovery that a simple mathematical principle can apply to such varied phenomena has inspired further exploration into the nature of self-organisation and emergent behaviour in complex systems. Zipf’s Law has thus become part of a broader body of work related to power laws, which have been identified in other domains, such as the distribution of wealth, stock market fluctuations, and the size of natural disasters.
In information theory, Zipf’s Law has played a pivotal role in the development of more efficient methods for handling and retrieving data. The knowledge that a few terms or items occur far more frequently than others has been crucial in optimising search engines, data compression algorithms, and information retrieval systems. For example, search engines use the principle behind Zipf’s Law to prioritise common queries, ensuring that frequently searched terms return the most relevant results quickly. Similarly, in text compression, understanding word frequency distributions allows for more efficient encoding methods, reducing the overall size of data files. The legacy of Zipf’s Law in information theory continues to shape the way we interact with vast amounts of data in the digital age.
In economics, Zipf’s Law has had a significant impact on the understanding of wealth distribution and market dynamics. The observation that income and wealth follow a Zipfian distribution in many societies has led to a deeper analysis of inequality and the concentration of resources in the hands of a few. This has implications for public policy and economic theory, influencing debates on taxation, wealth redistribution, and the mechanisms that drive financial inequality. The law’s ability to describe the unequal distribution of wealth across different economies underscores its importance in understanding economic systems at both micro and macro levels.
Zipf’s Law has also left a notable legacy in the study of urban populations and city growth. The rank-size rule, derived from Zipf’s Law, has been used to model the distribution of city sizes within countries, providing valuable insights into the processes that drive urbanisation and population concentration. Urban planners and geographers continue to use the law to study migration patterns, resource allocation, and the evolution of city networks. Its legacy in this field highlights the law’s relevance not only for theoretical research but also for practical applications in policy-making and infrastructure development.
Moreover, Zipf’s Law has influenced the study of networks and social systems, where the principle of least effort, which underpins the law, helps explain the distribution of connections or interactions within a network. In social media platforms, for instance, a small number of users typically generate the majority of content, while most users remain relatively inactive. Similarly, in network theory, Zipf’s Law explains why some nodes in a network become highly connected hubs while others have fewer connections. These insights have significant implications for understanding the flow of information, the spread of influence, and the resilience of networks to disruption.
Despite its broad applicability, Zipf’s Law is not without its limitations, and part of its legacy includes the ongoing debate over its generalisability. While the law describes many systems remarkably well, there are instances where deviations from the Zipfian distribution occur, particularly in smaller datasets or highly controlled environments. This has led to the development of more nuanced models that adjust for these deviations, such as Mandelbrot’s Law, which refines Zipf’s original formulation to account for certain inconsistencies. Nonetheless, even these criticisms and refinements underscore the enduring relevance of Zipf’s work in stimulating further research and improving our understanding of complex systems.
The legacy of Zipf’s Law is also reflected in its influence on the broader concept of self-organising systems. Zipf’s observation that a simple, statistical rule can govern the structure of complex systems resonates with modern scientific paradigms that emphasise the role of self-organisation in everything from biological systems to economic markets. The law’s continued presence in scientific discussions about emergent behaviour and complexity theory demonstrates its long-lasting impact on how we conceptualise and study the world around us.